2021.05.22 - [AI/DL] - Backpropagation(역전파) - 가중치 업데이트 계산식 도출1
Backpropagation(역전파) - 가중치 업데이트 계산식 도출1
입력값과 은닉층 그리고 출력층에서 주어지는 수는 각각 2개씩이다. 가중치의 합은 $a$로 활성화 함수는 $\sigma$(sigmoid function)로 주어진다. $w_{31}$(출력층의 가중치)의 가중치 업데이트 계산식 도
patrickstar-jjh.tistory.com
이전 글에 이어서 이번에는 은닉층의 가중치를 업데이트 하는 계산식에 대해 알아보고자 한다.
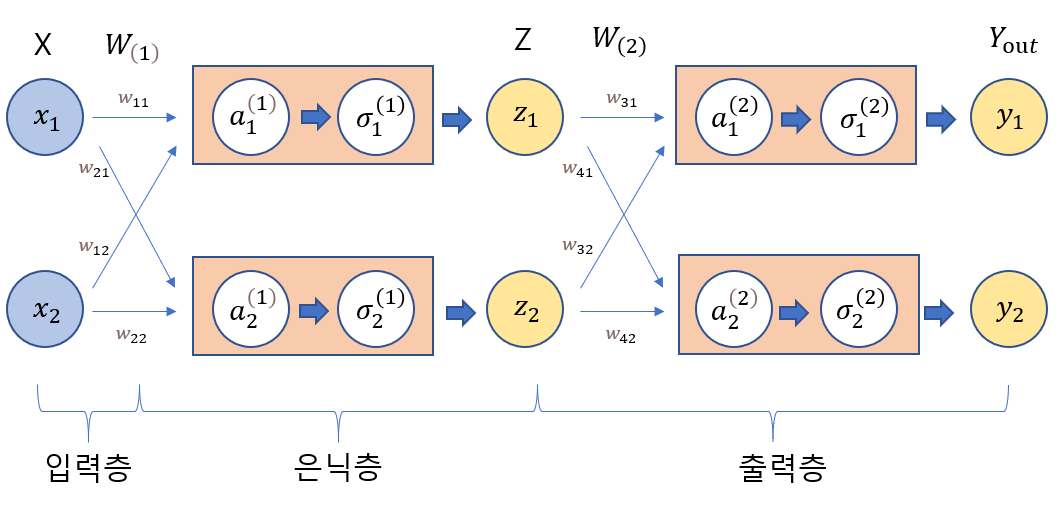
$w_{11}$(은닉층의 가중치)의 가중치 업데이트 계산식 산출
기초적인 식인 $w_{11}(t+1)=w_{11}(t)-\frac{\partial error}{\partial w_{11}}$에서 $\frac{\partial error}{\partial w_{11}}$를 구해야 한다.
체인룰에 의해 $\frac{\partial error }{\partial w_{11}}=$ $\frac{\partial error}{\partial z_{1}}$ $\cdot\frac{\partial z_{1}}{\partial a_{1}^{(1)}}$ $\cdot\frac{\partial a_{1}^{(1)}}{\partial w_{11}}$로 표현이 가능하다
2번째와 3번째 식은 출력층의 가중치 업데이트의 경우와 마찬가지로 다음과 같이 계산이 가능하다.
$\frac{\partial z_{1}}{\partial a_{1}^{(1)}}= z_{1}(1-z_{1})$ ( sigmoid 함수($\sigma(x)$)의 1차미분 참조, $\frac{\text{d} \sigma(x)}{\text{d}x}=\sigma(x)\cdot(1-\sigma(x))$)
$\frac{\partial a_{1}^{(1)}}{\partial w_{11}}=$ $x_{1}$ 이다
문제는 첫 번째 식인 $\frac{\partial error}{\partial z_{1}}$이다.
$error=\frac{1}{2}(y_{t1}-y_{1})^{2}+\frac{1}{2}(y_{t2}-y_{2})^{2}$ 인데 $z_{1}$은 $y_{1}$과 $y_{2}$의 형성에 모두 관여하므로 편미분을 하더라도 계산이 비교적 복잡해진다.
즉 $\frac{\partial error}{\partial z_{1}} = \frac{\partial error(y{1})}{\partial z_{1}} + \frac{\partial error(y{2})}{\partial z_{1}}$로 표현된다.
먼저 $y_{1}$에 관여하는 식을 보면
$\frac{\partial error(y{1})}{\partial z_{1}}=\frac{\partial error(y_{1})}{\partial a_{1}^{(2)}}\cdot\frac{\partial a_{1}^{(2)}}{\partial z_{1}}$에서
$\frac{\partial error(y{1})}{\partial a_{1}^{(2)}}=\frac{\partial error(y_{1})}{\partial y_{1}}\cdot\frac{\partial y_{1}}{\partial a_{1}^{(2)}}=(y_{1}-y_{t1})\cdot y_{1}\cdot (1-y_{1})$ 이고 ------ (출력층 가중치 업데이트 참조)
$\frac{\partial a_{1}^{(2)}}{\partial z_{1}}=w_{31}$이므로
$\frac{\partial error(y_{1})}{\partial z_{1}}=(y_{1}-y_{t1})\cdot y_{1}\cdot (1-y_{1})\cdot w_{31}$ 이고
$\delta_{y_{1}}=(y_{1}-y_{t1})\cdot y_{1}\cdot (1-y_{1})$ 라고 한다면(delta식)
최종적으로 $\frac{\partial error(y_{1})}{\partial z_{1}}=\delta_{y_{1}}\cdot w_{31}$이 된다.
똑같은 방식으로 $y_{2}$에 관여하는 식은
$\frac{\partial error(y{2})}{\partial z_{1}}=\frac{\partial error(y_{2})}{\partial a_{2}^{(2)}}\cdot\frac{\partial a_{2}^{(2)}}{\partial z_{1}}$에서
$\frac{\partial error(y{2})}{\partial a_{2}^{(2)}}=\frac{\partial error(y_{2})}{\partial y_{2}}\cdot\frac{\partial y_{2}}{\partial a_{2}^{(2)}}=(y_{2}-y_{t2})\cdot y_{2}\cdot (1-y_{2})$ 이고 ------ (출력층 가중치 업데이트 참조)
$\frac{\partial a_{2}^{(2)}}{\partial z_{1}}=w_{41}$이므로
$\frac{\partial error(y_{2})}{\partial z_{1}}=(y_{2}-y_{t2})\cdot y_{2}\cdot (1-y_{2})\cdot w_{41}$ 이고
$\delta_{y_{2}}=(y_{2}-y_{t2})\cdot y_{2}\cdot (1-y_{2})$ 라고 한다면(delta식)
최종적으로 $\frac{\partial error(y_{2})}{\partial z_{1}}=\delta_{y_{2}}\cdot w_{41}$이 된다.
즉 $\frac{\partial error}{\partial z_{1}} = \frac{\partial error(y{1})}{\partial z_{1}} + \frac{\partial error(y{2})}{\partial z_{1}} = \delta_{y_{1}}\cdot w_{31}+\delta_{y_{2}}\cdot w_{41} $이므로
$\frac{\partial error }{\partial w_{11}}=$ $\frac{\partial error}{\partial z_{1}}$ $\cdot\frac{\partial z_{1}}{\partial a_{1}^{(1)}}$ $\cdot\frac{\partial a_{1}^{(1)}}{\partial w_{11}}=$ $(\delta_{y_{1}}\cdot w_{31}+\delta_{y_{2}}\cdot w_{41})\cdot z_{1}(1-z_{1})\cdot x_{1}$ 이다.
$(\delta_{y_{1}}\cdot w_{31}+\delta_{y_{2}}\cdot w_{41})\cdot z_{1}(1-z_{1}) = \delta_{h}$(은닉층의 델타식)라고 한다면
최종적으로 $\frac{\partial error }{\partial w_{11}}=\delta_{h}\cdot x_{1}$이 된다.
<References>
모두의딥러닝(조태호, 길벗)
'datascience > DL' 카테고리의 다른 글
| Backpropagation(역전파) - 코드로 구해보기 (0) | 2021.06.06 |
|---|---|
| Backpropagation(역전파) - 출력층 가중치 업데이트 계산식 도출 (0) | 2021.05.22 |
| 딥러닝 순전파 실습(퍼셉트론 계산과정) (0) | 2021.05.16 |