패트릭의 개발노트

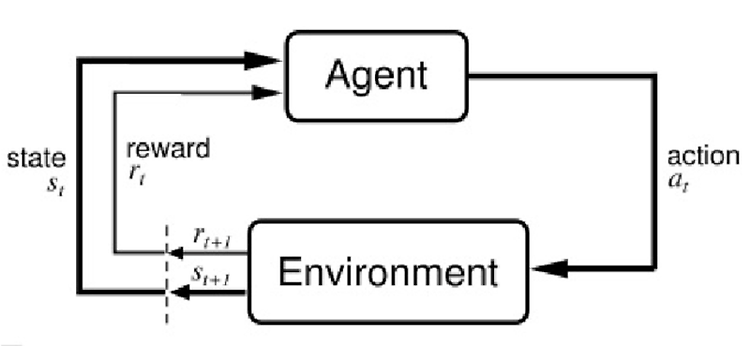
0단계: 재귀적 표현 $v_{\pi}(s_{t})=\mathbb{E}_{\pi}[r_{t+1}+\gamma v_{\pi}(s_{t+1})]$ $q_{\pi}(s_{t},a_{t})=\mathbb{E}_{\pi}[r_{t+1}+\gamma q_{\pi}(s_{t+1},a_{t+1})]$ 1단계: $v_{\pi}$와 $q_{\pi}$를 서로를 이용해 표현 $v_{\pi}(s) = \sum_{a\in A}\pi(a|s)q_{\pi}(s,a)$ $\Leftrightarrow s의 밸류 = \sum_{}(s에서 a를 실행할 확률) * (s에서 a를 실행하는 것의 밸류)$ $q_{\pi}(s,a)=r_{s}^{a}+\gamma \sum_{s'\in S}P_{ss'}^{a}v_{\pi}(s')$ $\Leftright..

GridWorld 구현 import random import numpy as np class GridWorld(): def __init__(self): self.x=0 self.y=0 def step(self, a): # 0번 액션: 왼쪽, 1번 액션: 위, 2번 액션: 오른쪽, 3번 액션: 아래쪽 if a==0: self.move_left() elif a==1: self.move_up() elif a==2: self.move_right() elif a==3: self.move_down() reward = -1 # 보상은 항상 -1로 고정 done = self.is_done() return (self.x, self.y), reward, done def move_right(self): self.y += 1..

강화학습(RL)에서 순차적 의사결정 문제 방법론에 대해 설명하는 마르코프 결정 프로세스의 기본 개념들을 정리해보고자 한다. ■마르코프 프로세스(MP) $$MP\equiv(S,P)$$ ■전이확률 : 상태s에서 다음 상태s'에 도착할 확률 $$P_{ss'}$$ ■마르코프 성질: 미래는 오로지 현재에 의해 결정된다 $$\mathbb{P}[s_{t+1}|s_{t}]=\mathbb{P}[s_{t+1}|s_{1},s_{2},...,s_{t}]$$ ■마르코프 리워드 프로세스(MRP) : MP에 보상 개념 추가 R: 보상함수, G:리턴, γ: 감쇠 인자 $$MRP\equiv(S,P,R,\gamma)$$ $$R=\mathbb{E}[R_{t}|S_{t}=s]$$ $$G_{t}=R_{t+1}+\gamma R_{t+2}+\g..